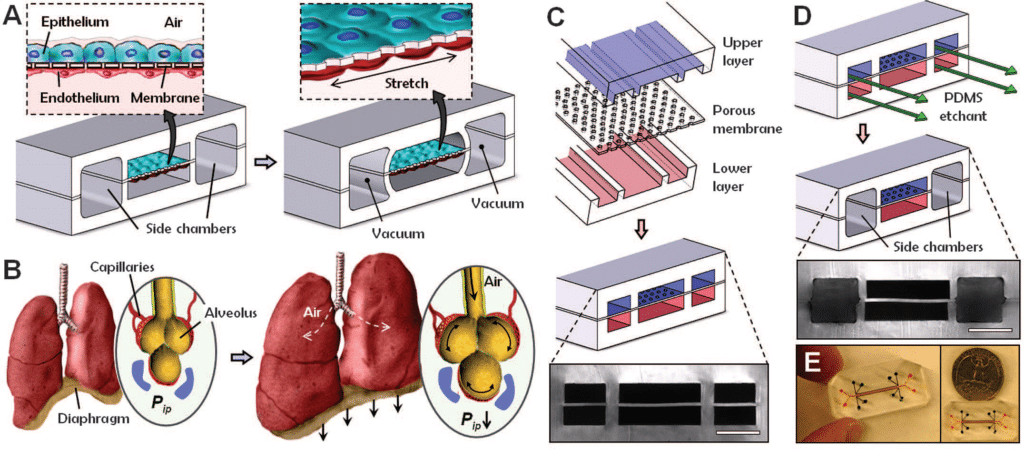
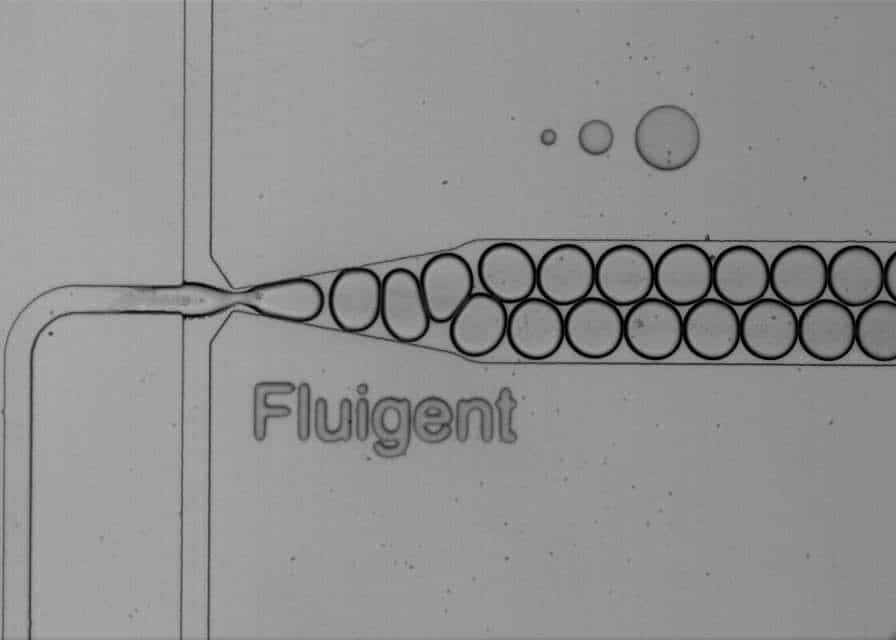
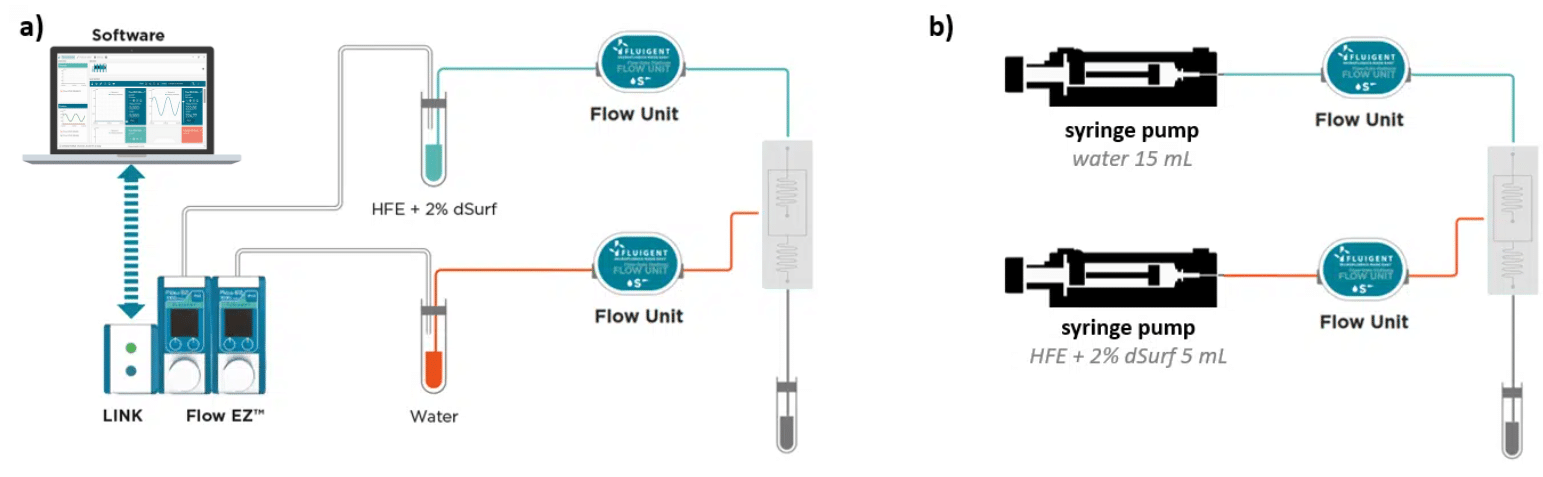
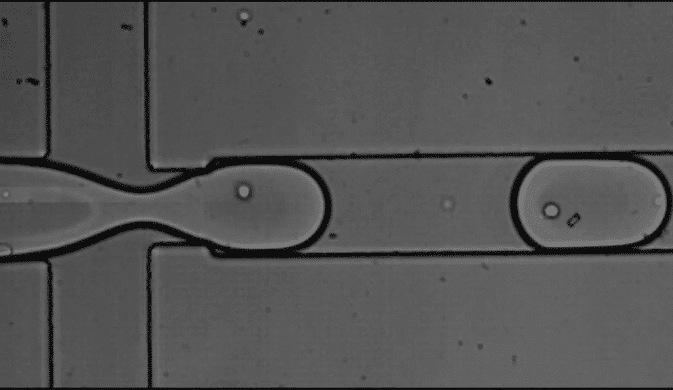
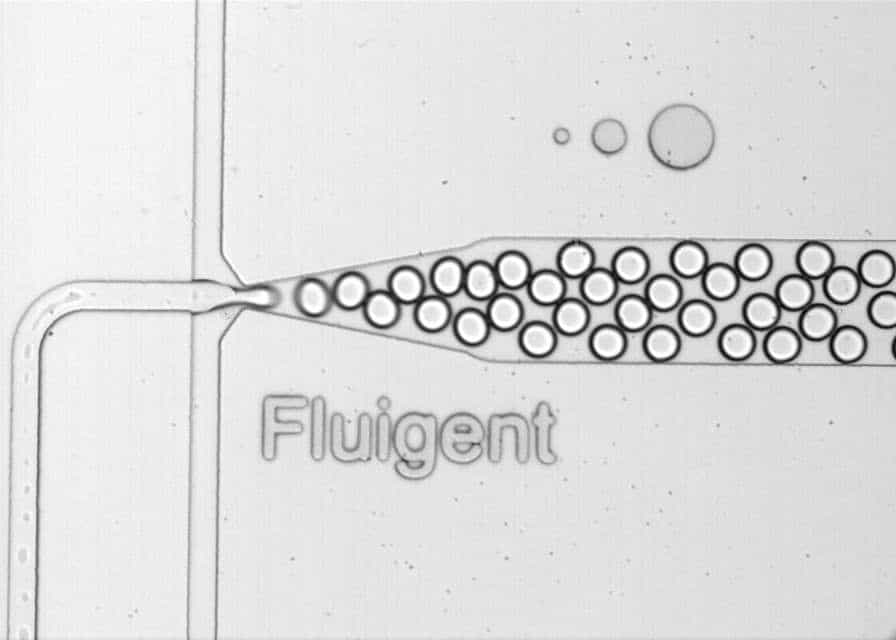
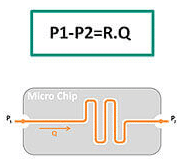
Expert Reviews: Basics of Microfluidics
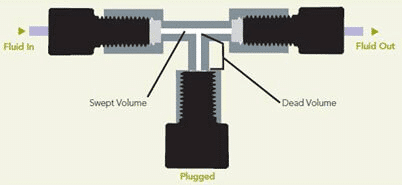
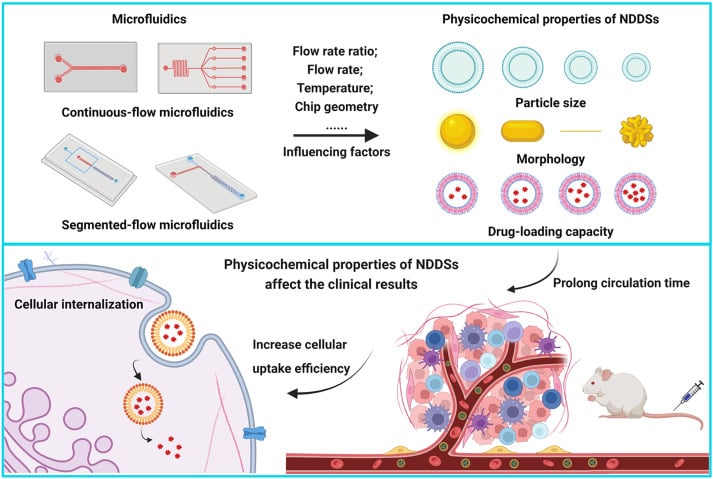
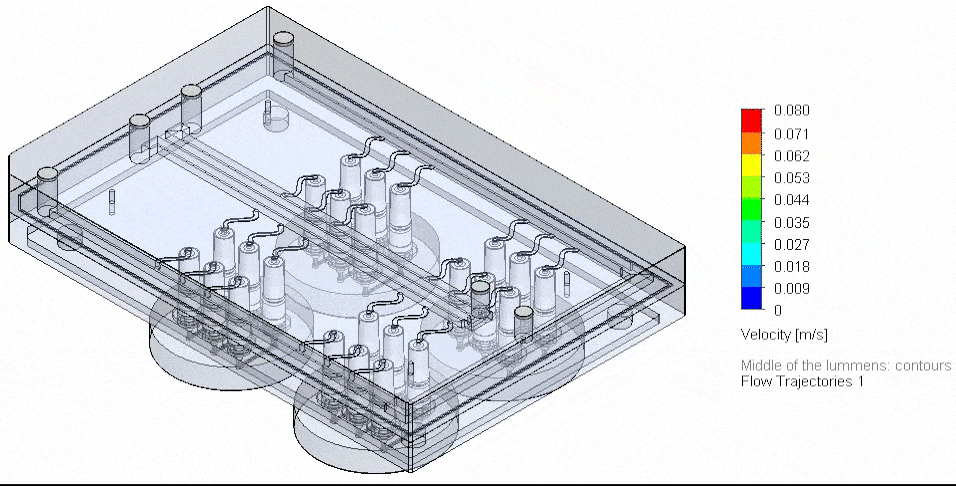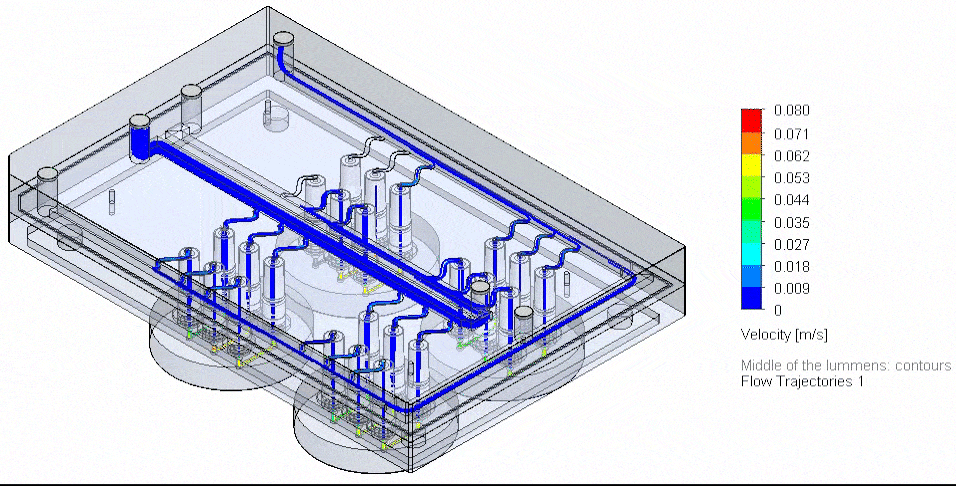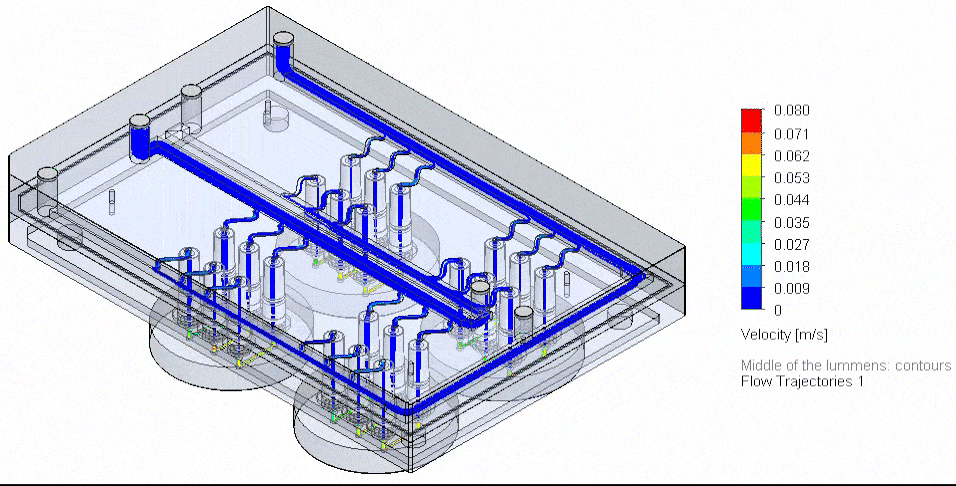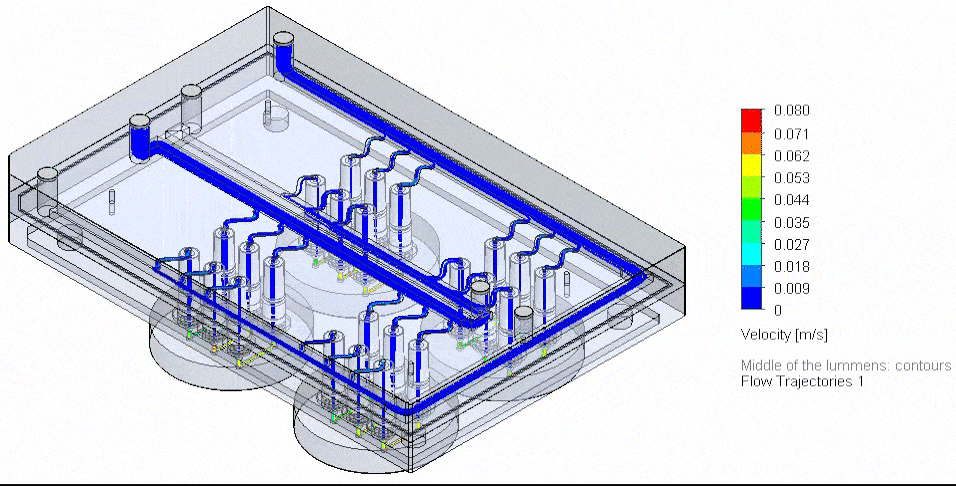
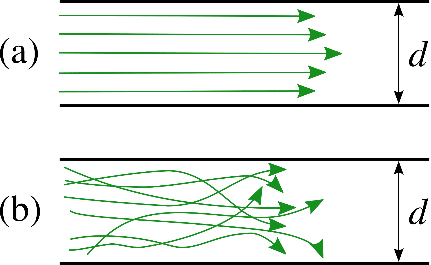
Microfluidics is defined as the science of fluid flow at a micrometric scale.It refers to a set of tools for manipulating fluids and materials at a scale of tens to hundreds of microns. Fluigent was the first company to introduce pressure-driven flow control to the microfluidic research market as opposed to conventional syringe and peristaltic pumps. As a pioneer in microfluidics, we have set the standard in microfluidic control and strive to stay in the forefront of science. We have created content about the concepts, physics and basics of microfluidics, the elements of a microfluidic system, the advantages of pressure based flow controller devices over traditional methods, and experiments related to application in organ on a chip, cell culture, microencapsulation, and droplet and particle generation. You will also find the latest and most innovative techniques in microfluidic cell biology, comparative studies, and industrial/OEM to share with the scientific community.