Why Control Shear Stress in Cell Biology?
Shear stress in cell biology plays a dual role. On one hand, it should be minimized during the in vitro handling of cells and organoids to prevent cell damage. In-vivo, many cells, including endothelial cells from blood vessels and epithelial cells in kidney, intestine, liver - are constantly exposed to shear conditions from blood flow, which is essential for healthy cellular organization and gene expression. Therefore, carefully quantifying and reproducing the shear stress is important for in vitro assays and organ modeling experiments.
Shear stress physical definition
Shear-stress is a tangential force applied on a surface. Fluid shear stress depends on fluid velocity and viscosity. Therefore, it can be simplified in the case of Newtonian fluids as the following equation:
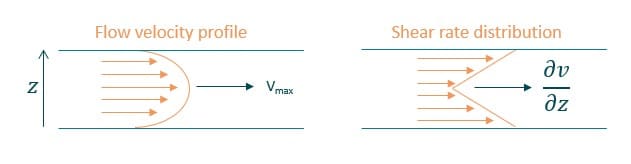
τ = η * (∂v/∂z)
where η is the viscosity (g/cm*s = Poise), ∂v/∂z is the velocity gradient or shear rate (s).
In a microfluidic channel with laminar flow, the velocity profile is parabolic. The maximum velocity at the center and the minimum at the channel walls. Resulting shear stress is highest at the walls and lowest at the center of the channel. (figure 1).
Use our Shear Stress Calculator to determine your experimental parameters. Define the flow rate or the pressure to be applied in your system, the dimension of microfluidic chip and tubing length to apply the correct controlled shear stress for your cell culture under flow conditions.
Shear Stress Effects on Cells
In common in-vitro experiments, cells are cultured on petri dishes with no media flow. This is an incomplete model that does not completely capture the cellular behavior. In living organisms, cells are continuously exposed to shear stress from fluid movement. Incorporating shear stress into in vitro systems is essential for several reasons:
- Mechanical Stimulation: Fluid flow produces a mechanical stimulus, that promotes cell elongation to the direction of the flow —especially in endothelial and other adherent cell cultures (Figure 2. Cell morphology and organization changes under shear stress) [1]
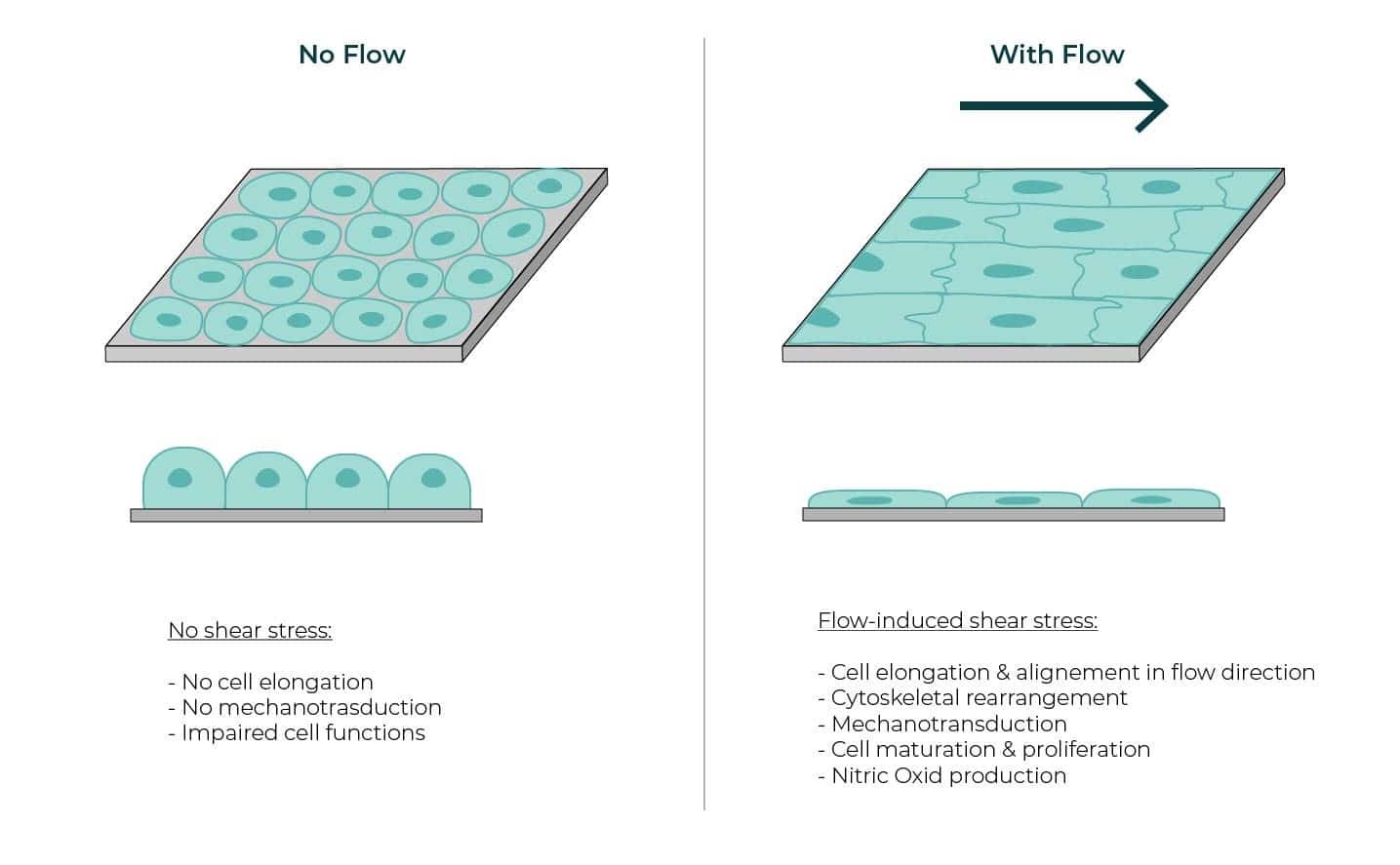
- Endothelial Cell Response: Endothelial cells are particularly responsive to shear stress, undergoing cytoskeletal remodeling [2]. This response helps maintain vascular homeostasis and influences processes such as angiogenesis and vessel remodeling [3]
- Cancer Cell Dynamics: In cancer research, shear stress is known to contribute to the metastatic cascade processes, such as extravasation and interstitial migration. The average intravascular speed of tumor cells under luminal flow has been observed to increase to ~ 12.5 μm/h, as compared to ~ 9.4 μm/h under static conditions [4].
- Improve Physiological Relevance and Precision: HUVECs cultured under laminar flow, compared to those under orbital flow, exhibit more physiologically relevant tissue factor expression [5].
- Tissue-Specific Shear Stress: Different tissues experience distinct physiological shear stress levels, which is important to consider when designing and modeling in vitro experiments.
| Cell types | Shear stress value (Pa) | Shear stress value (dyn/cm2) |
|---|---|---|
| Arteries [6] | 1-2 | 10-20 |
| Veins [6] | 0.1 -0.6 | 1-6 |
| Mouse embryonic kidney [7] | 0.04 – 0.5 | 0.4 – 5 |
| Human kidney [8] | 0.03 -0.12 | 0.3 -1.2 |
| Alveolar epithelial cells [9] | 0.4 -1.5 | 4 -15 |
How to Control Shear Stress in Cellular Microphysiological Systems
With the development of microfluidics, enabling precise control of flow rates and microchannel geometries, researchers are able to fine-tune the shear stress applied to cells. Early research demonstrated that specific levels of shear stress can influence endothelial cell structure and function [10].
Over the past 20 years, advancements in microfluidics have deepened our understanding of these effects. More recently, the development of organ-on-a-chip models—where functional tissues are cultured within microfluidic chips—has shown that controlled mechanical stimulation is crucial for regulating cell behavior and modulating responses to infectious agents and medicines [11].
Key variables for controlling shear stress include:
- Precise Flow Rate Control: Maintaining a stable and reproducible flow rate over long periods ensures consistent shear stress exposure.
- Microchannel Geometry: The shape, width, and height of microchannels directly influence shear stress distribution across the cells.
- Fluid Viscosity: The viscosity of the culture medium affects shear stress. Variations in BSA content, chemical additives and temperature can affect the media viscosity.
- Pulsatile vs. Steady Flow: Mimicking physiological conditions requires dynamic flow patterns (e.g., pulsatile or oscillatory flow).
- Cell Seeding Density and Adhesion: The confluence and attachment of cells impact their response to shear stress; optimizing seeding conditions ensures uniform exposure.
- Substrate Stiffness and Elasticity: The mechanical properties of the microfluidic chip substrate influence how cells perceive shear forces.
Related ressources
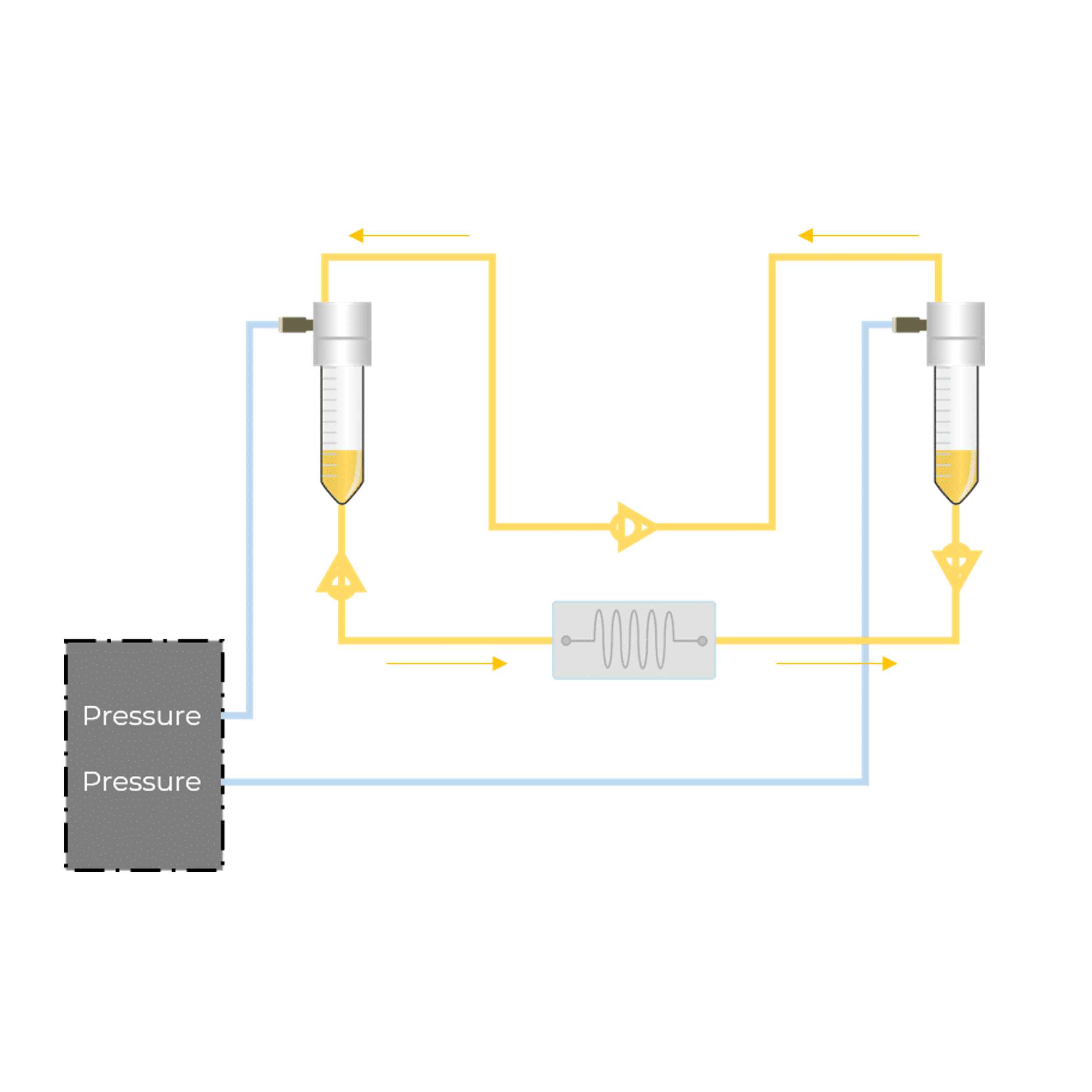
Microfluidic recirculation system
Read more- Support & Tools
Shear Stress Calculator
Read more - Microfluidic cell biology
Passive and active mechanical stimulation in microfluidic systems
Read more - Application notes
Development of a human gut-on-chip to assess the effect of shear stress on intestinal functions
Read more - Expert Reviews: Basics of Microfluidics
How to choose a microfluidic chip
Read more - Microfluidic cell biology
Mimicking in-vivo environments: biochemical and biomechanical stimulation
Read more - Microfluidics White Papers
A review of Organ on Chip Technology – A White Paper
Read more - Expert Reviews: Basics of Microfluidics
Flow Control Technologies: Comparison between peristaltic, syringe and pressure pumps for microfluidic applications
Read more
References
[1] Helmke B.P, Rosen A.B & Davies P.F. Mapping mechanical strain of an endogenous cytoskeletal network in living endothelial cells. Biophys J (2003). doi: 10.1016/S0006-3495(03)75074-7
[2] Malek A.M & Izumo S. Mechanism of endothelial cell shape change and cytoskeletal remodeling in response to fluid shear stress. J Cell Sci (1996). doi: 10.1242/jcs.109.4.713
[3] Campinho P, Vilfan A, Vermot J. Blood flow forces in shaping the vascular system: a focus on endothelial cell behavior. Front Physiol (2020) doi: 10.3389/fphys.2020.00552
[4] Hajal, C., et al. The effects of luminal and trans-endothelial fluid flows on the extravasation and tissue invasion of tumor cells in a 3D in vitro microvascular platform. Biomaterials (2021). doi: 10.1016/j. biomaterials.2020.120470
[5] Rochier A., et al. Laminar shear, but not orbital shear, has a synergistic effect with thrombin stimulation on tissue factor expression in human umbilical vein endothelial cells. J Vasc Surg (2011). doi: 10.1016/j.jvs.2011.01.002
[6] Lipowsky H.H., et al. The distribution of blood rheological parameters in the microvasculature of cat mesentery. Circ Res. (1978). doi: 10.1161/01.res.43.5.738
[7] Kimura H., et al. Effect of fluid shear stress on in vitro cultured ureteric bud cells. Biomicrofluidics (2018). doi: 10.1063/1.5035328.
[8] Ross E.J., et al. Three dimensional modeling of biologically relevant fluid shear stress in human renal tubule cells mimics in vivo transcriptional profiles. Sci Rep (2021). doi: 10.1038/s41598-021-93570-5
[9] Flitney E.W., et al. Insights into the mechanical properties of epithelial cells: the effects of shear stress on the assembly and remodeling of keratin intermediate filaments. FASEB J (2009). doi: 10.1096/ fj.08-124453
[10] Dewey C.F Jr. et al. The dynamic response of vascular endothelial cells to fluid shear stress. J Biomech Eng (1981). doi: 10.1115/1.3138276.
[11] Thompson et al. Mechanical Stimulation: A Crucial Element of Organ-on-Chip Models. Frontiers in Bioengineering and Biotechnology (2020). doi: 10.3389/fbioe.2020.602646